Free Description: What İs The Domain Of The Square Root Function Graphed Below?

What İs The Domain Of The Square Root Function Graphed Below? All answer and details below. Good reading.

What İs The Domain Of The Square Root Function Graphed Below?

What İs The Domain Of The Square Root Function Graphed Below?

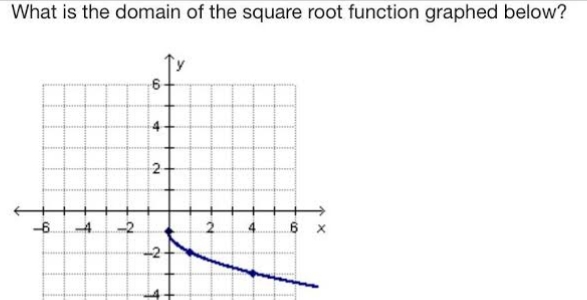
we know that

the domain of the square root function graphed is equal to

the interval——> [3,∞)

the domain is all real numbers for

What İs The Domain Of The Square Root Function Graphed Below?

the range of the square root function graphed is equal to

the interval——> [1,∞)

the range is all real numbers for $f(x)\geq 1$

therefore

the answer is the option

What İs The Domain Of The Square Root Function Graphed Below? We want to determine the range and range of the F function of X = sqrt 2 X minus four. However, there are several ways to do this, depending on how much we know about a particular function. If you’re more of a visual person, the best thing to do is to graph the function and then analyze the graph to determine the domain and range. Let’s start by doing this, and then we’ll use a second method to determine the domain and range. Whether you make a chart using technology or a table of values, the chart will appear in the video.

What İs The Domain Of The Square Root Function Graphed Below? Answer continues. Remember, domain is a set of all possible X values occurring along the horizontal axis and range is a set of all possible Y values and Y values occurring along the vertical axis. To determine the area graphically, we want to project the function onto the X-axis or determine how the function behaves horizontally. What I mean by this is to determine the domain. Notice how the leftmost point of the function will be here.

When X equals positive two, and from there on all X values shift or increase to the right. So the domain will be from positive 2 approaching positive Infinity. And we can express this in two ways. We can say that X is greater than or equal to two. Or, using range notation, we can say the range from 2:00 to Infinity is closed to two or includes 2. So we have a parenthesis here. What İs The Domain Of The Square Root Function Graphed Below?

And then it works in parentheses for Infinity and then for the range we want to project the graph onto the Y axis or how the function behaves vertically. Note that when y equals 0, the lowest point on this graph will be right here. And from here, the chart continues to move upwards, though it moves to the right quite quickly. So the range will be from zero to positive Infinity.

Along the Y axis. That is, the range must be greater than or equal to Y equals 0. Or, using range notation, we can say the range from zero to Infinity, where zero is closed and we have a parenthesis on Infinity. But of course it takes some time to graph the function, so we can use what we know about the square root to determine the domain and range without the graph. Let’s see if we can do this?

What İs The Domain Of The Square Root Function Graphed Below? We know that to calculate a square root, the root or the number below the square root must be greater than or equal to 0. It cannot be negative because it gives an imaginary number. So if we assume that two X -, 4 must be greater than or equal to zero, we can solve this inequality and find the domain like this. So if we add 4 to both sides we get 2X.

Greater than or equal to positive four. Then we divide both sides in half. Notice that X, which is actually the domain of our function, stays with greater than or equal to two. And then, if we take the square root of a number, assuming that the smallest value we can get will be 0, and that every other value must be a positive number, i.e. our function, or Y. What İs The Domain Of The Square Root Function Graphed Below?

It must always be greater than or equal to 0. Again, when we take the square root of a number, it will always be greater than or equal to 0. It will never be negative and Y will never be greater than or equal to 0. So if you can reason with domain and range based on what you know about a particular function, you may find that it will be much faster. But if you are unsure, my advice is to plot a graph of the function and then analyze the behavior of the graph. What İs The Domain Of The Square Root Function Graphed Below? Video below.

https://brainly.com/question/10331931

5/5 - (1 vote)