Use The Drawing Tools To Graph The Solution To This System Of Inequalities On The Coordinate Plane

Use the drawing tools to graph the solution to this system of inequalities on the coordinate plane. We will inform you with all the details and pictures. We have also left the video narration for you below.

Use the drawing tools to graph the solution to this system of inequalities on the coordinate plane

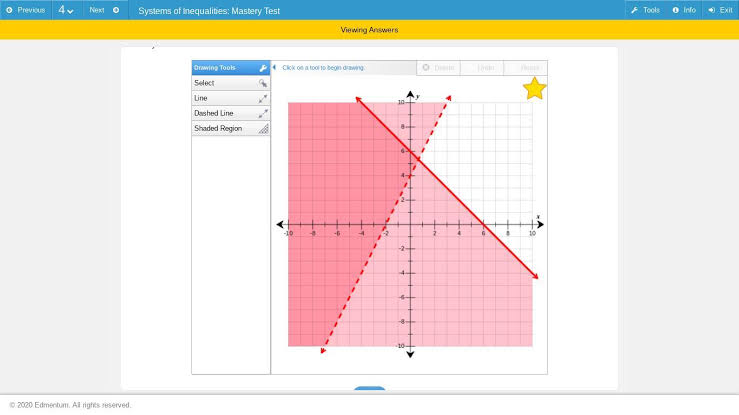
Use the drawing tools to graph the solution to this system of inequalities on the coordinate plane. y > 2x + 4 x + y ≤ 6.

The solution region for the given pair of inequalities is found to be the common shaded region in the graph attached.

Step-by-step explanation:

We know if the sign of inequality contains ‘=’, the graph of the inequality is drawn with the help of a solid line but if the sign of inequality does not contains ‘=’, the line of the graph of inequality is dotted.

Use the drawing tools to graph the solution to this system of inequalities on the coordinate plane: For drawing the graph of any inequality, we first have to assume the inequality as an equation and draw the graph of the resulting equation. Hence, finding the points for the inequality , we let the inequality as:

Putting y=0, we get:

The point will be: (-2,0)

Now, putting x=0, we get:

The point will be: (0,4)

Now as the sign of inequality is >, the line of graph will be dotted.

Taking a test point (0,0) to find the shaded region, substituting this in the inequality,

Use the drawing tools to graph the solution to this system of inequalities on the coordinate plane

So, the shaded region will be away from the test point.

Similarly, finding the points for the inequality , we let the inequality as:

Putting y=0, we get:

The point will be: (6,0)

Now, putting x=0, we get:

The point will be: (0,6)

Now, as the sign of inequality is of , the line of graph will be solid.

Use the drawing tools to graph the solution to this system of inequalities on the coordinate plane – Taking a test point (0,0) to find the shaded region, substituting this in the inequality,

So, the shaded region will be towards the test point.

The resulting graph is attached after the solution.

The solution to the pair of given inequalities will be the shaded region that is common between both the individual inequality’s shaded regions. / Use the drawing tools to graph the solution to this system of inequalities on the coordinate plane.

Ok, let’s take a look at the graphic in the video and take it one step further. Let’s start by seeing the solution graphs of inequality systems. So let’s try one right away and see how we did it. Let’s solve for X less than minus one, little two, and also 0, little Y less than or three. And I want to see what the solution set for this thing looks like.

Use the drawing tools to graph the solution to this system of inequalities on the coordinate plane: So this first step is to draw some axes. Let’s draw some axis. Ok, that’s not very exciting. So unexciting. Well, what I’m going to do now is, I’m going to graph these two things separately. So let’s take a look at this. Now the first thing I’m going to say is OK, now X if X = -1, where is that? What’s this? So X = -. 1 is a vertical line. All places where x = -, 1 would be right here.

And so I put a vertical line and because I saw a = I was allowed to actually add it. Actually, I’ll include it. Solidify, type X equals -, 1. Okay, now the other possibility is X = 2. Now X = 2. Of course here, 1-2. This is – 1.

Use the drawing tools to graph the solution to this system of inequalities on the coordinate plane: But notice that I have a strict inequality. I’m going to put a dotted line over there, a dotted vertical line to represent the right side. Now, where do I fill it? Where will I fill the items? Well, now notice, I actually have three zones and I have to think about where to fill it. Well, you can think about it and see, X is between minus one and two. So which X’s are between minus one and two? All right, these X’s are here. So actually these should be the X’s that provide it. So I’m going to shade it. Use the drawing tools to graph the solution to this system of inequalities on the coordinate plane.

So I shade these X’s and therefore any Y that has an X between minus one and two. And by the way, this means that I can include this line. I can touch that line, but I cannot touch this line. I can get as close as I want, but I can’t touch it. Definitely less than two. Now what about the Y thing? All right, Y is greater than 0 but less than or equal to three. So what would it look like if I graphed it? Well, if I were to graph that.

Use the drawing tools to graph the solution to this system of inequalities on the coordinate plane: Y = 0 is just the X axis and I need to put a dotted line there. Although technically right on it, I think I’d put that kind of appreciation on top of it. But to show you that it’s dotted, to remind you that it’s not actually included and then Y is less than or equal to three, I’m going to put it like this, so I need to get three out of 123 and let’s put a straight horizontal line to equal 3.

Right across, solid. And where do I fill it now? I want all values where the y’s are between these two. So this would be right here in this group. So actually, now I’m going to paint this in color, this tape is right over there. So what is the solution set for this? Well, you can see that they overlap. So it would actually be this small rectangular region.

Use the drawing tools to graph the solution to this system of inequalities on the coordinate plane: I can include this edge and include this edge, but I do not include this edge and I do not include this edge. So I add these parts but not these parts. These are dotted. This is the solution. And sometimes really, you know, you can write some sort of solution and point right in this area. Do you see where they overlap? Is it the solution? Ok, let’s try another one. It’s actually kind of fun. I think they’re fun. I hope you do too.

What do you say about this? Three X + 2 Y is greater than or equal to 1 and X + 2 Y is less than minus one. Well, the first thing I’m going to do here is actually just write these equations. By the way, you can write them in point slope form or use them in standard form as they are, but imagine equal signs here.

Use the drawing tools to graph the solution to this system of inequalities on the coordinate plane: If you want to graph these as they are and not solve anything, let me show you a really slick way of graphing these things. The helpful thing I’d look at for the first one is 3X plus two y = 1. Now how would this graph? All right, all I have to do is plant my axes and you know what I’m going to do? I’ll just find the intersections.

So, let’s say how do I find the Y-intercept? This is where x = 0. So let X = 0 and solve for Y. Look, I immediately see y = 1/2, so I know it’s past this point at 1/2. So we have 1/2 here. Suppose this is 1. So I’m at 1/2.

Use the drawing tools to graph the solution to this system of inequalities on the coordinate plane – And let’s see what the X value is. What is the X value? The value we cut off the x-axis is where y=0. So put a zero there and I immediately see X = 1/3. You see, actually these things are pretty easy to graph and I just combine them. I see I have greater or equal, so I’m allowed to put a straight line here. Durable. So I have this chart right now.

Use the drawing tools to graph the solution to this system of inequalities on the coordinate plane: The question is, should I shade up or down? Well, let’s think about it. Let’s put 00 and see if it satisfies it. If I enter 00, I see that zero is greater than or equal to 1. This is wrong. So this area should not exist. This must be the area I want. So I would overshadow them all. Or you could use some kind of hi-tech, because I have it so I’ll use it. If you got it, flaunt it. So actually, this would be the area where I would shade it. OK, what about next?

Graphic. The next graph is also a line. Let’s see what their intersection is. Use a different color. I’m going to use this color now. Let’s see what I would see if X were zero? Y is equal. Y has to be equal. Convince that there is a =. Y must equal minus 1/2, minus 1/2. And so I’d see that I’d go down to negative 1 over 2.

Use the drawing tools to graph the solution to this system of inequalities on the coordinate plane: And what happens? What is the X-intercept? Well, if I look at this Y IS0I and see that X is equal to -, 1. So I see that X is equal to -, 1. So this point is there. Now I will connect them together. Let’s be careful now. There is a strict inequality here. Since there is a strict inequality, that means I have a dotted line. There is a dotted line here because I am not allowed to include this limit.

It’s a strict inequality, so we definitely want it. Wherever the border is, we know we won’t include it.

https://brainly.in/question/27920585

5/5 - (2 votes)