Best Description: Which Statements Are True Check All That Apply

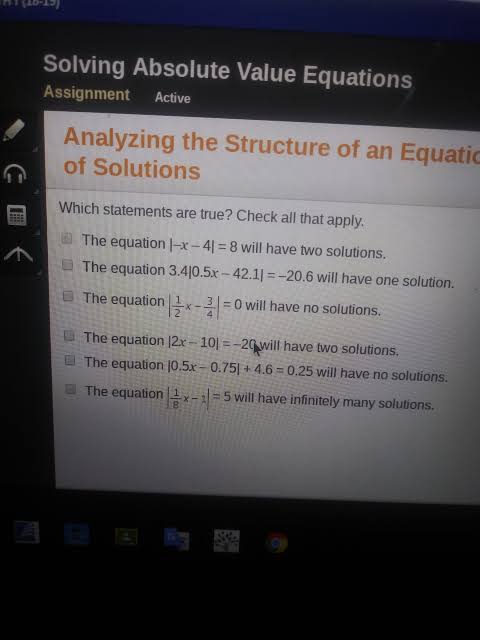
Which Statements Are True Check All That Apply. We give you the answer to your question, both in video and in writing. We wish you good work.

Which Statements Are True Check All That Apply

Which statements are true? Check all that apply. On a coordinate plane, point A is (2, 3), point B is (3, 2), point C is (negative 2, 2), point D is (negative 3, negative 3), point E is (0, 3), point F is (2, 0), and point G is (0, 0). A is in Quadrant I. B is on the x-axis. C is in Quadrant I. D is in Quadrant III. E is on the x-axis. F is on the x-axis. G is on the y-axis.

Answer: A D F

Step-by-step explanation:

A is in Quadrant 1
D is in Quandrant 3
F is on the X-axis
I also got it right on Edgeunity

Which Statements Are True Check All That Apply: We also shared the transcription of the sounds in the video for you: The question here is to ask which statements are correct regarding undefined terms in geometry. Check all that apply. So we are not given any statement here. I want to use.

You knew which one was right. His answer to clarify. There are three undefined geometry terms, point, line, plane. This is true. So the wording was missing here. So it is given here. The first statement is incorrect because a point has no dimension. The second statement is false because a plane has no definite beginning and end. The third statement is true. The line has one dimension, so this is true. Explanation. The fourth statement is incorrect because a point specifies the location.

Which Statements Are True Check All That Apply: Statement 5 in the video is correct. A plane consists of an infinite set of 1. So all these statements are true, but we can’t really verify because we really aren’t. We don’t have any statements, but we’ll go over what that means in general. Its meaning is three undefined geometry terms. So first we have a point, then we have a line, and then we have a plane.

So 3 undefined terms. So this is something you have to memorize. So one point is pretty simple. There is only one point in space. A line is defined by two points. So if you have two points, you have a line. This is mainly because before you can define a function that covers these two points, you need to draw a line between them. Finally, for an airplane this is 3 points.

It is defined by three non-linear points. So what does that mean? It’s not linear. So to create alignment you need to have three points in space that don’t align with each other. If we had a diagram with xy then we would have XY.

Which Statements Are True Check All That Apply: We can’t let them be back-to-back so that this scenario would just be a line, not a plane, they could form a line. And so they cannot be collinear. They should be. It’s a little hard to imagine in 3D. So they should be something like this. They should be like 3 kinds of different points and they will form a plane. So if you connect these three dots, you have a plane.

In a 3D coordinate system, we have the points 1.2 and .3 and they form a plane because they are not collinear, otherwise if they were collinear then you would just make a line and if we only had .1 and .2 here, they are just a straight line would be. And then if we only had one point, it would just be a point on its own. These are the three undefined terms in geometry and their definitions. So we can’t really verify the statements, but somehow we have explained it. (Which Statements Are True Check All That Apply)

How accurate are these terms. To verify, the statement in question was not provided and we will mark it as correct.

Ok, thanks for attending this one-class session. I hope you found these answers to math problems helpful.

5/5 - (2 votes)